Category theory jargon for JavaScripters

If you are learning functional programming, you must hear monad or category theory and want to know what they are. You google it, find some Mystery diagram or complex math formula. It's too hard to comprehend. In this post, I explain some category theory terminology with JavaScript examples because category theory is a branch of math, you don't need to learn Haskell in order to understand it, just a litter bit of 'type notation.' I use type notation for javascript code. you can read it here

What is category theory?

Category theory is a field of abstract mathematics that studies relationships between things. We think about the relationships between two things, but then we think about the relationships between those relationships.

In category theory, we draw an arrow as a relationship between two things. If A, B is two different cities, the relationship is that there is a road from A to B. Maybe we have two different roads of getting here. So two arrows F and G are two different roads. The relationship between route F and G could be comparing by time. Mathematicians call city A, G Object, and call arrow morphisms. Category theory is an ultimate abstraction. The object can represent anything, even a category; morphism can represent any relationship. To make things more practical, Mathematicians impost artificial restrictions – category law.

1. idenrify: Composing with the identity doesn’t do anything.

  compose(id, f)  == f  // left identity
  compose(f, id)  == f  // right identity

2. associativity. that means the order of composition doesn't matter

compose(compose(f, g), h)  == compose(f, compose(g, h)) 

Note: Object have nothing to do with the JavaScript Object. This may be confusing the first time you read it. They are not the same thing. Object in category represents any type, but Javascript object type is one of them.

Example: The category of sets

Object A, B is two sets, arrow is a function between sets, The identity morphism is the identity function, and composition is given by composition of functions.

Programmers think of morphisms as functions. An object is a type, which is a set of values. The function takes a type return a type as a relationship between two types. Type just a set of values. Int type is a set of numbers from negative infinity to positive infinite. toString function is a morphism in the category of sets. toString :: Int -> Strng

What is a functor?

Suppose I had two different categories. How are those objects in each category related between two categories? The arrow between them is called a functor.

A functor is a structure-preserving map object and morphism from one category to another. For example, A functor F : C → D takes each object x in C to an object in D; similarly, send morphism in C to D. object x in C become Fx, morphism f :: a -> b become Ff :: Fa -> Fb.

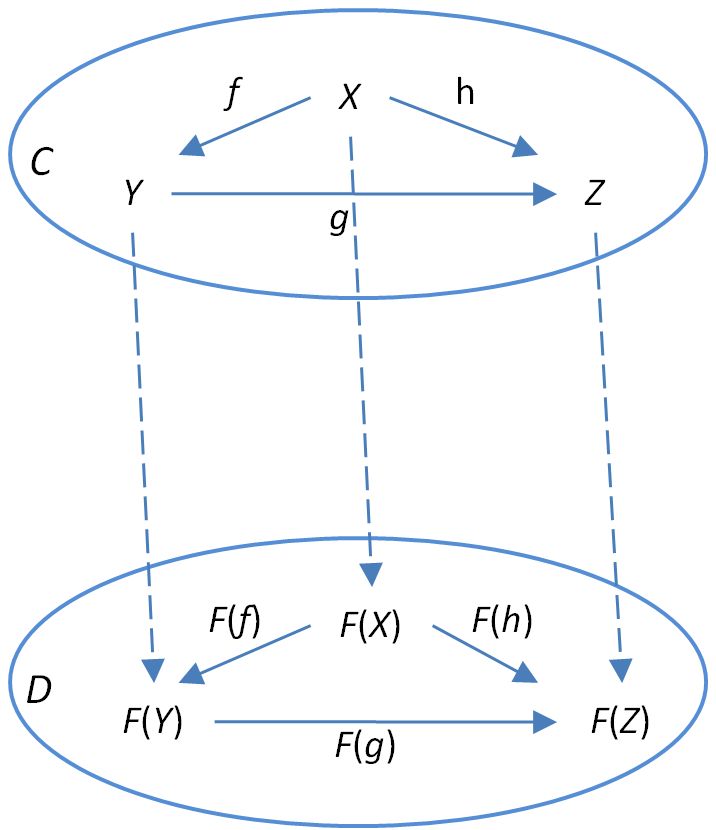
In programming, the most common functor just deals with a single category(type and function). C and D can be the same category that is called endofunctor. A functor is a construction function that acts on type, which means you take a type and define a type base on that type. send morphism in C to D is another function (a -> b) -> (a -> fb). in Haskell it's called fmap. this process is lot of words to explain. Usually, people say: A functor data type is something you can map over.

Against, functor preserve object and arrow(the relationship). in programming, type construction function preserve object. map function preserve arrow

JavaScript built-in Array looks like a functor. Constructing an array, we could say new Array("new value"). Think of Array is in another category D. Passing some arguments to it is the same as map a to Array(a). The Array is a functor if it also maps morphism. Can we define define a function ArraySayHI :: Array a -> Array b?

    var a = “Mirror”
    var Arraya = new Array(a)  -- sent a to Category D
    var b = “Hi mirror”
    var arrayb = new Array (b) – sent b to category D
              var sayHi = str = “HI” ++ str
    // define arraySayHi
    Var arraySayHi = arraya => arraya.map(sayHi)

The built-in array method map act on array value. We can define the mapped version of sayHi that means the array is a functor ①Array is a data structure. Do you mean functor is some data type? Yes! Indeed, a functor in programming is a data type that depends on other data types. We can say New Array(a) is a type that depends on type a(string in this example). ② What are map doing in arraySayHi? map function, which helps us mapping morphisms, lift function sayHi to the array. We give a arraya; it gives back arrayb. If you map on array, like [1,2,3].map(addOne), you are Using functoriality of array There's another way of looking at functor, saying functor is sort of like a container for a value. An array contains some value. You can modify it by map over it. That's people say functor are some container you can map over.

Lift

What is lifting? Well, lifting is the same as mapping function to another category. Mathematics calls it lifting a function. Look at the up arrow on the image, the category C below arrow lifts up to the top. For functor F, we might say that it lifts f to F( f ).

Create you own functor in Javascript

Again, a functor is a function create some data type that has map method depends on another type. So what you need is ① a function take an argument, ② return a type that can contain a value. That's the object or array ③ define map method for object.. array already had a map method, you can skip this step ④ done

// ① create function 
var identityFunctor = value => ({  //② return object
  value = value,
  map (fn) {return identifyFunctor(fn(value)})  // ③ map method modifying valur
})

Thinking in a category way object/array is functor map value to another category Instead of store multiple values in a single variable. Think of the map method as lifting a function instead of modifying value and return a new object/array.

Natural transformation?

If two functor maps to the same category, are they related to each other? The arrow mapping between the functor is called natural transformation.

Monad

everyone wants to know what a monad is; the monad is a way of composing embellished functions. We can easily compose two functions is those input type is same as output type. What happens if the input type is different from the output type? How to compose those functions?

foo1: num -> [num, string]
foo2: num -> [num, string] 

Function foo1 returns an array with num and string; one way to handle it is that Destructuring the array, pass num to foo2, then Destructuring result and combine two string. That is what monad does.

function compose(f1, f2) {
  return val => {
    var [num, str] = f1(val)
    var [num2, str2 = f2(num)
    return [num2, str ++ str2]
  } 
}

Create a monad

Monad includes two parts

1. a way to put value to structures. let of = val => [val, '']
2. a way to remove structures and extract value, this is the compose function. compose funtion can be rewrited to ([num, string], f2) => {...} this form of function is called flatMap, bine, then. JavaScript Promise implements map and then through then, so it is a functor and a monad.

What is the problem monad solve?

In functional programming function is pure, thing like input-output/modify statue is not pure. Computing that has side effects can be converted into pure calculations and replace regular functions with embellished functions. In the upper example, num is the calculated result, string is side effects. Side effects only happen in some structures (array here), not modify the outside world.

Wrapping up

Relationships between categories are known as functors, and relationships between functors are known as natural transformation Functor is a function construct new type depends on the old type, or a container you can map over. Monad is a way of composing embellished functions.